记录高数一些常用需要记忆的公式
常用等价无穷小
当$x\to 0$时:
$$
\begin{aligned}
&\sin x \sim \tan x \sim x\\
&\arcsin x \sim \arctan x \sim x\\
& \mathrm{e}^x-1 \sim \ln{(1+x)} \sim x\\
&a^x-1\sim x\ln {a}\\
&1-\cos x\sim \frac{1}{2}x^2\\
&(1+x)^a\sim ax\\
&x-\ln{(1+x)}\sim \frac{1}{2}x^2\\
&x-\sin x\sim \arcsin x-x\sim \frac{1}{6}x^3\\
&\tan x-x\sim x-\arctan x\sim \frac{1}{3}x^3\\
&\tan x-\sin x\sim \arcsin x-\arctan x\sim \frac{1}{2}x^3
\end{aligned}
$$
基本求导公式
$$
\begin{aligned}
&C'=0(C为常数)\\
&(x^\alpha )'=\alpha x^{\alpha -1}\\
&(\sin x)'=\cos x\\
&(\cos x)'=-\sin x\\
&(\tan x)'=\sec ^2x\\
&(\cot x)'=-\csc ^2x\\
&(\sec x)'=\sec x\tan x\\
&(\csc x)'=-\csc x\cot x\\
&(a^x)'=a^x\ln a\\
&(\mathrm{e}^x)'=\mathrm{e}^x\\
&(\arcsin x)'=\frac{1}{\sqrt{1-x^2} } \\
&(\arccos x)'=-\frac{1}{\sqrt{1-x^2} }\\
&(\arctan x)'=\frac{1}{1+x^2} \\
&(\operatorname{arccot} x)'=-\frac{1}{1+x^2}
\end{aligned}
$$
复合函数求导
设 $y = f(u)$ , $u = \varphi(x)$ ,如果 $\varphi(x)$ 在 $x$ 处可导,$f(u)$ 在对应点 $u$ 处可导,则复合函数 $y = f[\varphi(x)]$ 在 $x$ 处可导, 且有
$$
\frac{\mathrm{d} y}{\mathrm{d} x} = \frac{\mathrm{d} y}{\mathrm{d} u} \frac{\mathrm{d} u}{\mathrm{d} x} = f^{\prime}[\varphi(x)] \varphi^{\prime}(x) \text { (链式法则). }
$$
反函数求导
设 $x = \varphi(y)$ 是 $y = f(x)$ 的反函数, 则
$$
\frac{\mathrm{d} x}{\mathrm{d} y} = \varphi'(y) = \frac{1}{f'(x)} , 其中 f'(x) \neq 0 .
$$
隐函数求导
设 $y = y(x)$ 是由方程 $F(x, y) = 0$ 所确定, 把 $F(x, y) = 0$ 两边的各项对 $x$ 求导, 把 $y$ 看作中间变量,用复合函数求导公式计算,然后再解出 $y’$ 的表达式.
$$
F_{x}^{\prime}+F_{y}^{\prime} \frac{\mathrm{d} y}{\mathrm{~d} x} = 0 \Rightarrow \frac{\mathrm{~d} y}{\mathrm{~d} x} = -\frac{F_{x}^{\prime}}{F_{y}^{\prime}}\left(F_{y}^{\prime} \neq 0\right)
$$
莱布尼兹公式
若$u(x)$,$v(x)$均$n$阶可导,则
$$
(uv)^{(n)}=\sum _{i=0}^n C_n^iu^{(i)}v^{(n-i)},其中u^{(0)}=u,v^{(0)}=v
$$
常用的麦克劳林公式
$$
\begin{aligned}
&\mathrm{e}^{x} = 1+x+\frac{x^{2}}{2!}+\cdots+\frac{x^{n}}{n!}+o\left(x^{n}\right) \\
&\sin x = x-\frac{x^{3}}{3!}+\cdots+\frac{(-1)^{n-1} x^{2 n-1}}{(2 n-1)!}+o\left(x^{2 n-1}\right) \\
&\cos x = 1-\frac{x^{2}}{2!}+\cdots+\frac{(-1)^{n} x^{2 n}}{(2 n)!}+o\left(x^{2 n}\right) \\
&\ln (1+x) = x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\cdots+(-1)^{n-1} \frac{x^{n}}{n}+o\left(x^{n}\right) \\
&(1+x)^{m} = 1+m x+\frac{m(m-1)}{2!} x^{2}+\cdots+\frac{m(m-1) \cdots(m-n+1)}{n!} x^{n}+o\left(x^{n}\right)
\end{aligned}
$$
渐近线
水平浙近线
若$\underset{x\to+\infty} \lim f(x) = b$ $\left(或 \underset{x\to -\infty}\lim f(x) = b\right)$, 则$y = b$为函数$y = f(x)$的水平渐近线.
垂直渐近线
若$\underset {x \to x_{0}^+}\lim f(x)=\infty$ $\left(或\underset{x \to x_{0}^-}\lim f(x) = \infty \right)$,则$x = x_{0}$为函数$y= f(x)$的垂直渐近线.
斜浙近线
若$k =\underset{x \to+\infty}\lim \frac{f(x)}{x}, b = \underset{x \to+\infty}\lim [f(x)-k x]$ $\left(或 k = \underset{x \to-\infty}\lim \frac{f(x)}{x}, b = \underset{x \to-\infty}\lim [f(x)-k x]\right)$, 则直线$y = k x+b$是曲线$y = f(x)$的斜浙近线.
基本积分公式
$$
\begin{aligned}
(1)&\int x^{k} \mathrm{~d} x = \frac{x^{k+1}}{k+1}+C(k \neq-1).\\
(2)&\int \frac{1}{x} \mathrm{~d} x = \ln |x|+C.\\
(3)&\int a^{x} \mathrm{~d} x = \frac{a^{x}}{\ln a}+C.\\
&\int \mathrm{e}^{x} \mathrm{~d} x = \mathrm{e}^{x}+C.\\
(4)&\int \cos x \mathrm{~d} x = \sin x+C.\\
&\int \sin x \mathrm{~d} x = -\cos x+C.\\
(5)&\int \frac{1}{\sin x} \mathrm{~d} x = \int \csc x \mathrm{~d} x = \ln |\csc x-\cot x|+C.\\
&\int \frac{1}{\cos x} \mathrm{dx} = \int \sec x \mathrm{~d} x = \ln |\sec x+\tan x|+C.\\
(6)&\int \frac{1}{\sin ^{2} x} \mathrm{dx} = \int \csc ^{2} x \mathrm{~d} x = -\cot x+C.\\
&\int \frac{1}{\cos ^{2} x} \mathrm{~d} x = \int \sec ^{2} x \mathrm{~d} x = \tan x+C.\\
(7)&\int \tan x \mathrm{~d} x = -\ln |\cos x|+C.\\
&\int \cot x \mathrm{~d} x = \ln |\sin x|+C.\\
(8)&\int \sec x \tan x d x = \sec x+C.\\
&\int \csc x \cot x \mathrm{~d} x = -\csc x+C.\\
(9)&\int \frac{1}{a^{2}+x^{2}} \mathrm{dx} = \frac{1}{a} \arctan \frac{x}{a}+C.\\
&\int \frac{1}{1+x^{2}} \mathrm{~d} x = \arctan x+C.\\
(10)&\int \frac{1}{\sqrt{a^{2}-x^{2}}} \mathrm{~d} x = \arcsin \frac{x}{a}+C.\\
&\int \frac{1}{\sqrt{1-x^{2}}} \mathrm{dx} = \arcsin x+C.\\
(11)&\int \frac{1}{a^{2}-x^{2}} \mathrm{~d} x = \frac{1}{2 a} \ln \left|\frac{a+x}{a-x}\right|+C.\\
&\int \frac{1}{1-x^{2}} \mathrm{~d} x = \frac{1}{2} \ln \left|\frac{1+x}{1-x}\right|+C.\\
(12)&\int \frac{1}{\sqrt{x^{2} \pm a^{2}}} \mathrm{~d} x = \ln \left|x+\sqrt{x^{2} \pm a^{2}}\right|+C .
\end{aligned}
$$
变限积分求导
若$f(x)$在$[a, b]$上连续,$\varphi(x)$, $\psi(x)$在$[a, b]$上可导, 则
$$
\left(\int_{\psi(x)}^{\varphi(x)}f(t)\mathrm{d}t \right)_{x}'=f[\varphi(x)] \varphi'(x)-f[\psi(x)]\cdot \psi'(x)
$$
定积分的常用结论
奇(偶)函数在对称区间上的积分
设 $f(x)$ 在 $[-l,l]$ 上连续,则
$$
\int_{-l}^{l} f(x) \mathrm{d} x=\left\{\begin{array}{ll}
0, &当f(x)为奇函数, \\
2 \int_{0}^{l} f(x) \mathrm{d} x, &当f(x)为偶函数.
\end{array}\right.
$$
周期函数的定积分
设 $f(x)$ 是以 $T$ 为周期的连续函数,$a$ 为任意实数,则
$$
\int_{a}^{a+T}f(x)dx=\int_{0}^{T}f(x)dx=\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)dx .
$$
华里士点火公式
$$
\begin{aligned}
\int_{0}^{\frac{\pi }{2} } \sin^{n} x =\int_{0}^{\frac{\pi }{2} } \cos^{n} x=\begin{cases}
\frac{n-1}{n}\times \frac{n-3}{n-2}\times \dotsb\times \frac{1}{2}\times\frac{\pi}{2},&n为大于1的正偶数, \\
\frac{n-1}{n}\times \frac{n-3}{n-2}\times \dotsb\times \frac{2}{3}\times 1 ,&n为大于1的正奇数.
\end{cases}
\end{aligned}
$$
常见反常积分的敛散性
$$
\begin{aligned}
&\int_a^{+\infty}\frac{1}{x^p}\mathrm{d}x\left\{\begin{array}{ll}
收敛, &p>1, \\
发散, &p\le1
\end{array}\right. \ (a>0).\\
\\
&\int_a^{+\infty}\frac{1}{x\ln^px}\mathrm{d}x\left\{\begin{array}{ll}
收敛, &p>1, \\
发散, &p\le1
\end{array}\right. \ (a>1).\\
\\
&\int_a^b\frac{1}{(x-a)^p}\mathrm{d}x\left\{\begin{array}{ll}
收敛, &p<1, \\
发散, &p\ge1.
\end{array}\right.
\end{aligned}
$$
平面图形面积
(1)直角坐标系
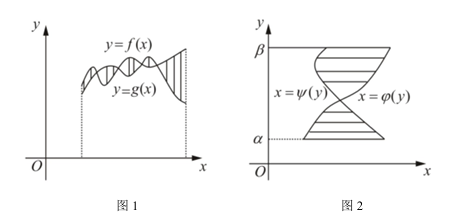
如图1所示的面积为 $S_1=\int_a^b|f(x)-g(x)|\mathrm{\ d}x$.
如图2所示的面积为 $S_2=\int_{\alpha}^{\beta}|\varphi(x)-\psi(x)|\mathrm{\ d}y$.
(2)极坐标系
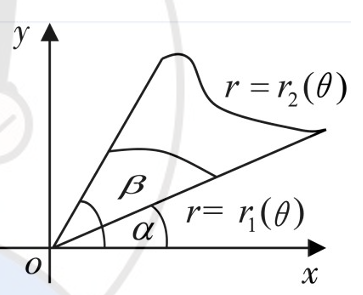
$$
S=\frac{1}{2}\int_{\alpha}^{\beta}\left[r_2^2(\theta)-r_1^2(\theta)\right]\mathrm{~d}\theta.
$$
旋转体体积
平面图形由曲线 $y=y(x)$ 与直线 $x=a$ ,$x=b$ 和 $x$ 轴围成,则
绕 $x$ 轴旋转一周所形成的旋转体的体积 $V_x=\pi \int_a^by^2(x)\mathrm{\ d}x$.
绕 $y$ 轴旋转一周所形成的旋转体的体积 $V_y=2\pi \int_a^bx|y(x)|\mathrm{\ d}x$.
二元函数取极值的充分条件
设 $z=f(x, y)$ 在点 $\left(x_{0}, y_{0}\right)$ 的某邻域内有连续的二阶偏导数, 且
$$
\begin{aligned}
&f_{x}'\left(x_{0}, y_{0}\right)=0, f_{y}'\left(x_{0}, y_{0}\right)=0 ;\\
&A=f_{x x}''\left(x_{0}, y_{0}\right), B=f_{x y}''\left(x_{0}, y_{0}\right), C=f_{y y}''\left(x_{0}, y_{0}\right) .
\end{aligned}
$$
(1) 若 $A C-B^{2}>0$ , 则 $\left(x_{0}, y_{0}\right)$ 是 $z=f(x, y)$ 的一个极值点, 且当 $A>0$ 时, $\left(x_{0}, y_{0}\right)$ 为极小值点; 当 $A<0$ 时, $\left(x_{0}, y_{0}\right)$ 为极大值点.
(2) 若 $A C-B^{2}<0$, 则 $\left(x_{0}, y_{0}\right)$ 不是 $z=f(x, y)$ 的极值点.
(3) 若 $A C-B^{2}=0$, 则无法判定 $\left(x_{0}, y_{0}\right)$ 是否为极值点, 此时应考虑利用极值点的定义进行判断。
二重积分
(1) 选择坐标系
直角坐标系下的二重积分表示: $\iint_{D} f(x, y) \mathrm{d} \sigma=\iint_{D} f(x, y) \mathrm{\ d} x \mathrm{\ d} y$.
极坐标系下的二重积分表示: $\iint_{D} f(x, y) \mathrm{d} \sigma=\iint_{D} f(r \cos \theta, r \sin \theta) r \mathrm{\ d} r \mathrm{\ d} \theta$.
(2) 二重积分的化简
(1) 如果积分区域 $D$ 关于 $x$ 轴对称,则二重积分
$$
\iint_{D} f(x, y) \mathrm{d} \sigma=\left\{\begin{array}{ll}
0, & f(x,-y)=-f(x, y), \\
2 \iint_{D_{1}} f(x, y) \mathrm{d} \sigma, & f(x,-y)=f(x, y) .
\end{array}\right.
$$
其中, $D_{1}$ 为 $D$ 在 $y \ge 0$ 的部分.
(2) 如果积分区域 D 关于 y 轴对称, 则二重积分
$$
\iint_{D} f(x, y) \mathrm{d} \sigma=\left\{\begin{array}{ll}
0, & f(-x, y)=-f(x, y), \\
2 \iint_{D_{1}} f(x, y) \mathrm{d} \sigma, & f(-x, y)=f(x, y) .
\end{array}\right.
$$
其中, $D_{1}$ 为 $D$ 在 $x \ge 0$ 的部分.
(3) 如果 $D$ 关于直线 $y=x$ 对称, 则
$$
\iint_{D} f(x, y) \mathrm{d} \sigma=\iint_{D} f(y, x) \mathrm{d} \sigma=\frac{1}{2} \iint_{D}(f(x, y)+f(y, x)) \mathrm{d} \sigma .
$$
可分离变量方程
$$
f_{1}(x) g_{1}(y) \mathrm{d} x+f_{2}(x) g_{2}(y) \mathrm{d} y=0,
$$
分离变量两边同除 $g_{1}(y) f_{2}(x) \neq 0$, 得 $\frac{f_{1}(x)}{f_{2}(x)} \mathrm{d} x+\frac{g_{2}(y)}{g_{1}(y)} \mathrm{d} y=0$, 然后两边积分即可.
齐次方程
$$
y'=f\left(\frac{y}{x}\right),
$$
令 $u=\frac{y}{x}$, 则 $y=u x, y'=u+x \frac{\mathrm{d} u}{\mathrm{d} x}$, 于是原方程可化为
$$
u+x \frac{\mathrm{d} u}{\mathrm{d} x}=f(u) \Rightarrow \frac{\mathrm{d} u}{f(u)-u}=\frac{\mathrm{d} x}{x} \Rightarrow \int \frac{\mathrm{d} u}{f(u)-u}=\ln |x|+C .
$$
求出积分后,再以 $\frac{y}{x}$ 代替 $u$ ,便得所给齐次方程的通解。
一阶线性方程
$$
y'+p(x) y=q(x)
$$
求解公式: $y=\left[\int q(x) \mathrm{e}^{\int p(x) \mathrm{dx}} \mathrm{d} x+C\right] \mathrm{e}^{-\int p(x) \mathrm{dx}}$.
二阶常系数线性齐次微分方程
$y^{\prime \prime}+p y^{\prime}+q y=0$, 其中 $p, q$ 均为常数特征方程: $\lambda^{2}+p \lambda+q=0$,
(1) 当 $\lambda_{1}, \lambda_{2}$ 为互异实根时, 微分方程通解为 $y(x)=C_{1} \mathrm{e}^{\lambda_{1} x}+C_{2} \mathrm{e}^{\lambda_{2} x}$;
(2) 当 $\lambda_{1}=\lambda_{2}$ 时,通解为 $y(x)=\left(C_{1}+C_{2} x\right) \mathrm{e}^{\lambda_{1} x}$ ;
(3) 当 $\lambda=\alpha \pm i \beta$ (复根) 时, 通解为 $y(x)=\mathrm{e}^{\alpha x}\left(C_{1} \cos \beta x+C_{2} \sin \beta x\right)$.
二阶常系数线性非齐次方程
$$
y''+p y'+q y=f(x), 其中 p, q 均为常数
$$
通解的求解步骤:
(1) 求对应的齐次方程的通解 $Y(x)$;
(2) 用待定系数法求出非齐次方程的特解 $y^{*}(x)$;
(3) 写出非齐次方程的通解为 $y^{*}(x)+Y(x)$.
二阶常系数非齐次线性方程的非齐次项 $f(x)$ 与特解 $y^{*}$ 的关系
| $y’’+p y’+q y=f(x)$ |
$特解 y^{*}(x) 的形式$ |
$f(x)=P_{n}(x) \mathrm{e}^{(x)}$
其中 $P_{n}(x)$ 为 $x$ 的 $n$ 次多项式 |
$a$ 不是特征根,$y^{*}(x)=R_{n}(x) \mathrm{e}^{a x}$,
$a$ 是特征方程的单根,$y^{*}(x)=x R_{n}(x) \mathrm{e}^{a x}$
$a$ 是特征方程的重根,$y^{*}(x)=x^{2} R_{n}(x) \mathrm{e}^{a x}$
( $R_{n}(x)$ 为 $n$ 次多项式的一般形式) |
$f(x)=P_{n}(x) \mathrm{e}^{\alpha x} \sin \beta x$
或 $f(x)=P_{n}(x) \mathrm{e}^{\alpha x} \cos \beta x$
其中 $P_{n}(x)$ 为 $n$ 次多项式的一般形式 |
$y^{*}(x)=x^{k} \mathrm{e}^{\alpha x}\left[Q_{n}(x) \cos \beta x+W_{n}(x) \sin \beta x\right]$
$\alpha \pm i \beta$ 不是特征根,$k=0$
$\alpha \pm i \beta$ 是特征根,$k=1$
$Q_{n}(x), W_{n}(x)$ 为 $n$ 次多项式的一般形式) |
高于二阶的常系数线性齐次微分方程
$n$ 阶常系数线性齐次微分方程的一般形式是:
$$
\begin{aligned}
&y^{(n)}+p_{1} y^{(n-1)}+p_{2} y^{(n-2)}+\cdots+p_{n-1} y^{\prime}+p_{n} y=0 , \\
&其中 p_{i}(i=1,2, \cdots, n) 为常数.
\end{aligned}
$$
相应的特征方程为 $\lambda^{n}+p_{1} \lambda^{n-1}+p_{2} \lambda^{n-2}+\cdots+p_{n-1} \lambda+p_{n}=0$,
(1) 若特征方程有 $n$ 个不同的实根 $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}$
则方程通解 $y=C_{1} \mathrm{e}^{\lambda_{1} x}+C_{2} \mathrm{e}^{\lambda_{2} x}+\cdots+C_{n} \mathrm{e}^{\lambda_{11} x}$.
(2) 若 $\lambda _ 0$ 为特征方程的 $k$ 重实根 $(k \le n)$
则方程通解中含有 $(C_1 +C_2 x+\cdots +C_{k}x^{k-1})e^{\lambda_0 x}$.
(3) 若 $\alpha \pm i\beta$ 为特征方程的 $k$ 重共轭复根 $(2k\le n)$
则方程通解中含有$e^{\alpha x}\left[\left(C_1 +C_2 x+\cdots +C_{k}x^{k-1}\right)\cos \beta x+\left(D_1 +D_2 x+\cdots +D_{k}x^{k-1}\right)\sin \beta x\right]$.



